pythonでAkerunコントローラーのブザー音を周波数解析する

新卒FWエンジニアのnaritakuです。

この記事は Calendar for Akerun | Advent Calendar 2021 - Qiita の 10 日目の記事です。

弊社製品Akeurnコントローラーはブザーを内蔵しているのですが、新規FWの評価中にbeep音を出して再起動をする場面に遭遇しました。

ソースコードからではなく、評価時の動作からデバッグすることもあるのですが、この記事では新年の寅年にあやかり、たまたま録音していた当時の音をスペクトラムに変換し、再起動直前になっていたbeep音の周波数の特定をします。

解析する環境の準備
スペクトラムの表示
beep音のみの解析
最小二乗法で周波数を推定する
- どの程度正しい周波数なのか
  - ピークとして使った周波数の精度
音階とその周波数
参考

解析する環境の準備

iPhoneのボイスメモで録音したところ.m4a拡張子で、１チャンネルの音源が記録されていました。

解析する音源

普段の組み込み開発はc言語やjavascriptなどを使いますが、簡単に解析することを目標に、本記事ではpythonで実施します。 google colabratoryを使うとセットアップもほとんどせずに解析できます

colabratory内ではGoogleDriveにアップロードした音源の利用やpipでのライブラリのインストールもできます。

from google.colab import drive
drive.mount('/content/drive')
!pip install pydub

スペクトラムの表示

scipyのsignal.spectrogram()を使ってスペクトラムに変換します。

窓関数はピークの周波数を精度よく出したいため、ハミング関数を使います。

サンプリング数Nが２のべき乗であることで高速にフーリエ変換できます。今回はN=1024でのFFTをSTEP(=100)データずつずらしながら実施します。

from pydub import AudioSegment
from scipy import signal
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import Normalize

def loadAudio(filePath):
  audio = AudioSegment.from_file(filePath, "m4a")
  print("チャンネル数",audio.channels)
  print("サンプリング周波数",audio.frame_rate,"[Hz]")
  print("再生時間",audio.duration_seconds,"[s]")
  #１chのみの音源を取り出す
  samples = np.array(audio.get_array_of_samples())
  sample = samples[::audio.channels]
  return sample,audio.frame_rate


sound,frameRate = loadAudio("/content/drive/MyDrive/CTL.m4a")

N=1024
step=100

freqs, times, Sx = signal.spectrogram(sound, fs=frameRate, window='hamming',nperseg=N, noverlap=N-step,detrend=False, scaling='spectrum') # スペクトログラム変数


plt.figure()
f,ax = plt.subplots(figsize=(12,8))
im=ax.pcolormesh(times, freqs/1000, 10* np.log10(Sx), cmap='magma',norm=Normalize(vmin=-60, vmax=60))

ax.set_yscale('log')
ax.set_ylim(0.1,24)
ax.set_ylabel('Frequency[kHz]')
ax.set_xlabel('Time[s]')

pp=plt.colorbar(im)
plt.show()

チャンネル数 1
サンプリング周波数 48000 [Hz]
再生時間 4.378729166666667 [s]

f:id:photosynth-inc:20220104033319p:plain — beep音を含む録音データのスペクトラム

全体的に低周波の音が強くなっていますが、beep音の出ている3.0[s]近辺では特定の周波数の音が大きくなっていることが確認できます。

beep音のみのデータにトリミングして再度FFTを行い、上記の特定の周波数について求めていきます

beep音のみの解析

beep音が再生されている時間のみにトリミングしたデータを使います。

音源

Beep音を矩形窓とハミング窓を使って切り取りフーリエ変換します。

from pydub import AudioSegment
from scipy import signal
import numpy as np
import matplotlib.pyplot as plt


def loadAudio(filePath):
  audio = AudioSegment.from_file(filePath, "m4a")
  print("チャンネル数",audio.channels)
  print("サンプリング周波数",audio.frame_rate,"[Hz]")
  print("再生時間",audio.duration_seconds,"[s]")
  #１chのみの音源を取り出す
  samples = np.array(audio.get_array_of_samples())
  sample = samples[::audio.channels]
  return sample,audio.frame_rate

def fft(sample,frameRate):
  # 音声全体を1つの波形としてフーリエ変換
  sp = np.fft.fft(sample)
  f = np.fft.fftfreq(sample.shape[0], 1.0/frameRate)
  # 正の周波数部分だけにする
  f= f[:f.shape[0]//2]
  sp = sp[:sp.shape[0]//2]
  sp[0] = sp[0] / 2
  magnitude=np.abs(sp)
  return f,magnitude


# フーリエ変換する波形の表示

sample,frameRate=loadAudio("/content/drive/MyDrive/beep.m4a")

N=len(sample)
time=[i/frameRate for i in range(N)]
hamming=np.hamming(N) * sample

plt.figure(figsize=(16,16))
plt.subplot(2,1,1)
plt.plot(time,sample,label='Rectangular window')
plt.plot(time,hamming,label='Hamming window')
plt.xlabel('time [s]')
plt.ylabel('amplitude')
plt.legend()

# フーリエ変換とピークとなる周波数の表示
f,magnitude=fft(sample,frameRate)
f_h,magnitude_h=fft(hamming,frameRate)
maxi = signal.argrelmax(magnitude, order=100)
maxi_h = signal.argrelmax(magnitude_h, order=100)

plt.subplot(2,1,2)
plt.plot(f, magnitude)
plt.plot(f_h, magnitude_h)
plt.plot(f[maxi[0]],magnitude[maxi[0]],'ro',label='peak(origin)')
plt.plot(f_h[maxi_h[0]],magnitude_h[maxi_h[0]],'gx',label='peak(hamming)')
plt.yscale("log")
plt.xlabel('frequency [Hz]')
plt.ylabel('magnitude')
plt.legend()

チャンネル数 1
サンプリング周波数 48000 [Hz]
再生時間 0.18695833333333334 [s]

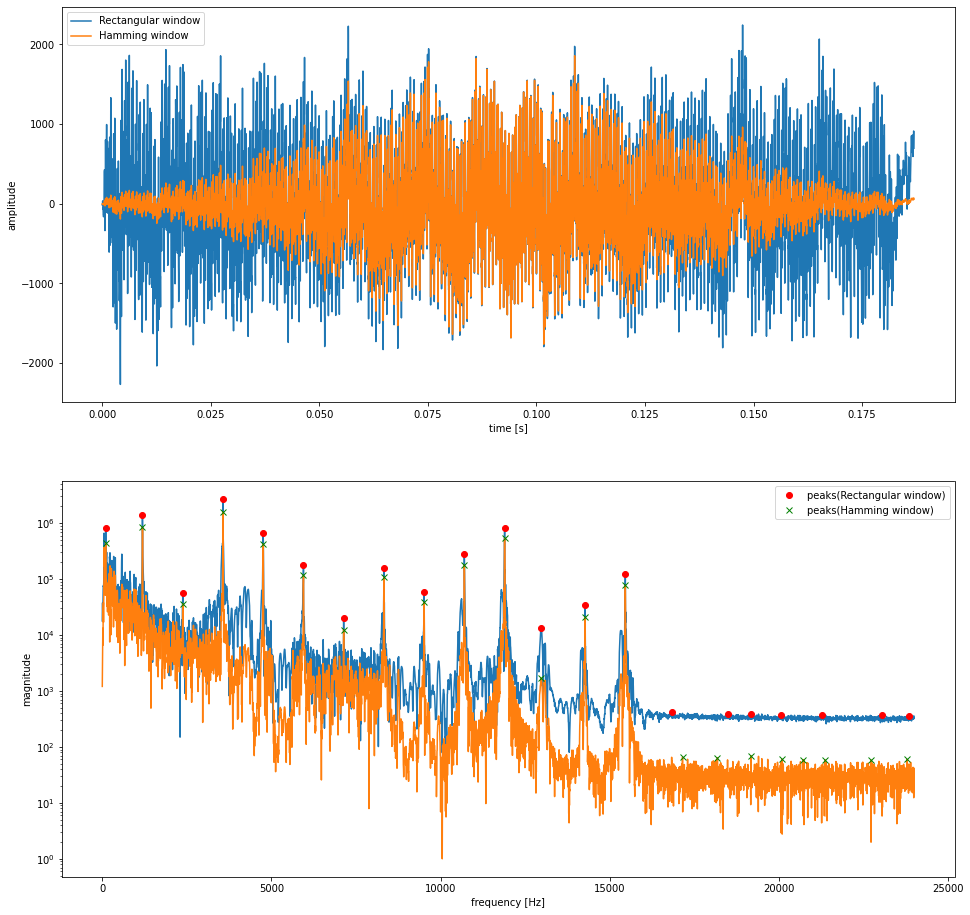
f:id:photosynth-inc:20220104042313p:plain — beep音の周波数解析

極大値かつ前後100点の中で最大値を取るものについて短形窓での極大値を赤丸、ハミング窓での極大値を緑Xでプロットすると、0Hzから16000[Hz]まではどちらも同じ周波数でピークが出ており、ピークとなる周波数ががほぼ等間隔になりました。 1100[Hz]あたりの音がブザーで鳴らしている周波数、それ以降のピークはブザーの倍音によるものである仮定のもと、ブザーの出力している周波数を推定します。

最小二乗法で周波数を推定する

求めたい周波数aのx倍の倍音の周波数がyとなる関数 y=ax についてaの値を最小二乗法で求めます。サンプルとして使う点は(x,y)=(0,0)と上記のグラフの赤丸でプロットされた2~13番目のピークの値とします。 (x,y)=(0,0)を使うのは0倍の時に0 [Hz]であることを期待しているためです。

# FFTの極大値から周波数を推定する

y=np.append(0, f[maxi[0][1:14]])
x=np.arange(len(y))
# y=mxとして最小二乗法
A = np.vstack([x, np.zeros(len(x))]).T
m, _ = np.linalg.lstsq(A, y, rcond=None)[0]


plt.plot(x,y,'gx',label='peaks of FFT(Rectangular window)')
plt.plot(x,m*x,label='Approximate line by least squares method')
plt.plot(1,m,'ro',label='Estimated frequency')
plt.xlabel('scale of tone')
plt.ylabel('frequency [Hz]')

plt.legend()

print("最小二乗法で推定した周波数", m,"[Hz]")

最小二乗法で推定した周波数 1187.9528242354183 [Hz]

f:id:photosynth-inc:20220104035206p:plain — 周波数の推定

グラフを見ても綺麗に倍音でピークになっていそうです。推定できた周波数は約1187[Hz]でしたが、Akerunコントローラーが出力しようとしていた音階を推測します。

どの程度正しい周波数なのか

かなりいい加減な解析をしているので、ピッタリ1187[Hz]の音源ではないはずです。現時点でどの程度信用できる周波数だったのか考えておきます。

ピークとして使った周波数の精度

今回のデータでは8974点のフーリエ変換を行なっていますが、サンプリング周波数48000[Hz]であるために、 $\frac{48000i}{8974} (i=0,1,2,...4987)$ [Hz]の波に変換しています。今回はピークとして使った周波数も約5.34[Hz]ごとに離散化されているため、本来の再生される周波数とたまたまサンプリングに使われる周波数が合致しなければ本来の周波数との誤差が生まれてしまいます。申し訳程度に最小二乗法でこの誤差が小さくなることを期待していますが、ピークとして使った周波数にすら信用できる区間が約5.34[Hz]の幅があることを念頭に入れておきましょう。

音階とその周波数

12平均律では $2^{\sqrt{12}}$ 倍の周波数で次の音階が得られるため、 440[Hz] をラ/A4 としたとき

ド♯/C♯6の周波数は約1109[Hz]
レ/D6の周波数は約1175[Hz]
レ♯/D♯6の周波数は約1245[Hz]

となります。

今回推定したピークとは10Hzほど低いものの、人間の耳ではbeep音はD6の音として聞こえることが想定され、当時slackで即レスをくれた音楽の得意なエンジニアと同じ結論になりました。これらをもとに、デバッグすることができそうですね。

f:id:photosynth-inc:20220109112402p:plain

参考

株式会社フォトシンスでは、一緒にプロダクトを成長させる様々なレイヤのエンジニアを募集しています。 hrmos.co

Akerun Proの購入はこちらから akerun.com